miliowl.blogg.se

1. Outcome of a coin flip for example crossword how to#
2. Outcome of a coin flip for example crossword series#

The first complete branch of the tree becomes the first row of the table. Example: Using a table, list all the possible schedules for the scenario in Exercise 9 in which Jacqueline takes Psychology section 1.

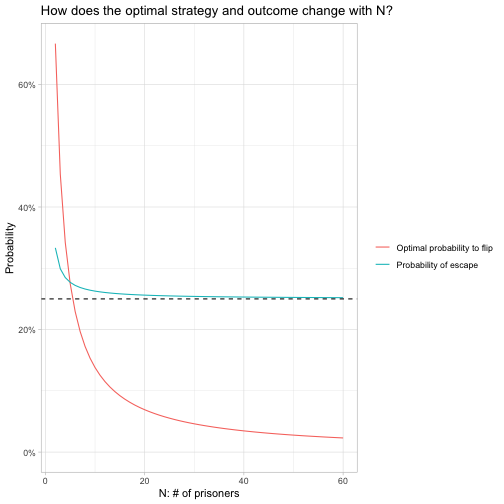
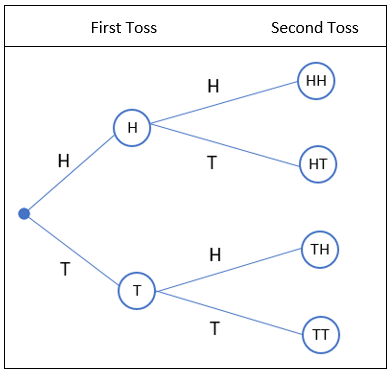
To get the outcomes, read along each branch of the tree to the end, and list the node labels. You can make a comma- separated list or table to list the outcomes. (Note: Depending on the exact information you are asked for, this step may be optional) Sometimes, you also want to know exactly what the possible outcomes are. Label the events at the end of each branch. Instructions: Complete the tree diagram below using the information in Exercise 6 in your Introductory Statistics textbook. There are 2 for psychology and A and P, and three for Spanish II. branches NOK Ono The numbered events are the section numbers she has to choose from. Psychology A and P Spanish | section section section 0 1 ON Start 12 End UN 000 000 000 000 GON GON -6 There are 12 possible outcomes. If there are two sections of psychology, two of A and P, and three of Spanish II, how many different class schedules can Jacqueline choose from? (Assume that the times of the sections do not conflict.) Label the starting point. This step ensures that you address each possible outcome.Įxample: Draw a tree diagram that shows all of the possible schedules for the scenario in Exercise 9 in your textbook, which is reproduced here: EXAMPLE 9 Multiplication Rule of Counting Jacqueline is in a nursing program and is required to take a course in psychology and one in physiology (A and P) next semester. (b) How many outcomes contain a head and a number greater than 4? (c) Probability Extension Assuming the outcomes displayed in the tree dia- gram are all equally likely, what is the probability that you will get a head and a number greater than 4 when you flip a coin and toss a die? Step 1: Draw the tree and label the branches. Tree Diagram (a) Draw a tree diagram to display all the possible outcomes that can occur when you flip a coin and then toss a die. Use a tree diagram to determine the number of outcomes for the scenario in Exercise 6 in your textbook, which is reproduced here: 6. If the outcomes consist of nonordered subgroups of r items taken from a group of n items, use the combinations rule, Cor n! C r!(n-r)! (10) A. If the outcomes consist of ordered subgroups of r items taken from a group of n items, use the permutations rule, P n! (9) (n-r)! 3. (b) How many outcomes contain a head and a number greater than 4? (c) Probability Extension Assuming the outcomes displayed in the tree dia- gram are all equally likely, what is the probability that you will get a head and a number greater than 4 when you flip a coin and toss a die? If the outcomes consist of nonordered subgroups of r items taken from a group of n items, use the combinations rule, n! r!(n - n)! (10) A. If the outcomes consist of ordered subgroups of r items taken from a group of n items, use the permutations rule, P.

Outcome of a coin flip for example crossword series#

If the experiment consists of a series of stages with various outcomes, use the multiplication rule of counting or a tree diagram.

Outcome of a coin flip for example crossword how to#

If not, use the following procedure to decide your approach: PROCEDURE How to determine the number of outcomes of an experiment 1. Sometimes, you will be told which method to use to determine the number of outcomes of an experiment. This worksheet will walk you through the steps to determine the number of outcomes of an experiment using a tree diagram or a rule/formula for permutations or combinations.

Computer the number of (non-ordered) groupings of outcomes using permutations. Compute the number of ordered arrangements of outcomes using permutations.